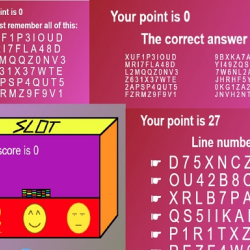
Control
Touch with mouse
description
Push your problem-solving prowess to the extreme with these deceptively straightforward yet demanding puzzles. Start by calculating the sum of all prime numbers between 1 and 100 that remain prime when their digits are reversed, then determine how many distinct integer solutions satisfy the equation \(3x + 7y = 42\) where both \(x\) and \(y\) are non-negative. Next, find the smallest positive integer divisible by 15 that becomes a perfect square when divided by 5. Tackle a geometric twist: A right triangle’s hypotenuse is twice the length of its shorter leg—compute the ratio of its area to the square of its longer leg without using decimal approximations. Finally, unravel a sequence challenge: What five-digit number follows 34159 in this pattern if each subsequent term is formed by multiplying the previous number’s digits and appending the result? No shortcuts—every solution demands rigorous logic and precision.